Chen Formula
Starting Hand Selection: Chen Formula : Sklansky Starting Hand Groups
The Chen formula is a system for scoring different starting hands in Texas Hold’em. It was created by Bill Chen for use in the book Hold’em Excellence by Lou Krieger. Bill Chen is also the guy that wrote The Mathematics of Poker.
The process looks a little tricky at first, but it’s really quite straightforward and logical after you have worked through a handful of examples.
The Chen formula.
- Score your highest card only. Do not add any points for your lower card.
- A = 10 points.
- K = 8 points.
- Q = 7 points.
- J = 6 points.
- 10 to 2 = 1/2 of card value. (e.g. a 6 would be worth 3 points)
- Multiply pairs by 2 of one card’s value. However, minimum score for a pair is 5.
- (e.g. KK = 16 points, 77 = 7 points, 22 = 5 points)
- Add 2 points if cards are suited.
- Subtract points if their is a gap between the two cards.
- No gap = -0 points.
- 1 card gap = -1 points.
- 2 card gap = -2 points.
- 3 card gap = -4 points.
- 4 card gap or more = -5 points. (Aces are high this step, so hands like A2, A3 etc. have a 4+ gap.)
- Add 1 point if there is a 0 or 1 card gap and both cards are lower than a Q. (e.g. JT, 75, 32 etc, this bonus point does not apply to pocket pairs)
- Round half point scores up. (e.g. 7.5 rounds up to 8)
For step 5, it’s easier to refer to this extra 1 point as a "straight bonus" to save confusion between steps 4 and 5. Subtracting 1 point for 1 gap and then adding it back again for lower cards seems a bit awkward I know, but that’s the way it works.
Chen Formula calculator.
Chen formula hand example scores.
- A
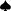 K
K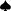
- A = +10 points.
- Suited = +2 points.
- Final score = 12 points.
- T
 T
T
- T = 10 x 1/2 = +5 points.
- Pair = multiply by 2.
- Final score = 10 points.
- 5
 7
7
- 7 = 7 x 1/2 = +3.5 points.
- Suited = +2 points.
- 1 card gap = -1 point.
- 0 - 1 card gap, both cards under Q = +1 point.
- Final score = 6 points. (5.5 points rounded up)
- 2
 7
7
- 7 = 7 x 1/2 = +3.5 points.
- 4+ card gap = -5 points.
- Final score = -1 point. (-1.5 points rounded up)
- A
 A
A
- A = +10 points.
- Pair = multiply by 2.
- Final score = 20 points.
So now we know how to work out how many points different hands are worth, what can we do with the numbers to help us with starting hand selection?
Using Chen formula hand points.
The main reason behind using the Chen formula for different starting hands was so that you can categorize them based on the Sklansky and Malmuth hand groups table.
That's all well and good for helping you to compare the strength of different starting hand in Hold'em, but it doesn't really do much in the way of strategy for starting hand selection. Therefore, I have done a little bit of work and created a starting hand strategy using the Chen formula.
Chen formula starting hand strategy.
- Only ever consider calling a raise with 10 points or more.
- Always raise or reraise with 12 points or more.
Short-handed strategy. (6 players)
Early position.
- Raise = 9 points or more.
- Fold = 8 points or less.
Mid position.
- Raise = 8 points or more.
- Fold = 7 points or less.
Late position.
- Raise = 7 points or more.
- Fold = 6 points or less.
Full-ring strategy. (10 players)
Early position.
- Raise = 10 points or more.
- Fold = 9 points or less.
Mid position.
- Raise = 9 points or more.
- Fold = 8 points or less.
Late position.
- Raise = 7 points or more.
- Fold = 6 points or less.
"Raise" = Raise if there have been no raises or calls before you.
"Fold" = Fold regardless if there has been a raise before you or not. Just fold.
About my Chen formula starting hand strategy.
As with any set of rules or guidelines in poker, this Chen formula starting hand strategy isn’t perfect and will have it’s flaws. However, I like to think that this is an easy-to-use and solid preflop strategy using the Chen formula.
Most of the strategy involves either raising or folding preflop, which is a solid approach to take as a new player and a style that you will grow accustomed to as your game progresses. The starting hand requirements are also a little tight, but that’s only to be expected if you’re using a guide and you haven’t quite found your feet when it comes to starting hand selection yet.
I took inspiration from the Chen formula article at SimplyHoldem.com (no longer active) to create this starting hand strategy. I decided to develop my own because I believe that the guidelines at Simply Holdem were flawed because:
- It does not distinguish between short and full ring games.
- Just calling the big blind is not a profitable way to play NL Hold’em for the most part.
Chen formula evaluation.
The Chen formula is never going to be a complete substitute for proper preflop starting hand strategy. It will also take a little getting used to if you want to work hand scores out on the fly. However, this is as good a formula as you are going to find for working out preflop starting hand strengths in NL Hold’em.
The starting hand strategy I worked out will also have its own flaws, but again this is as good as a simple guideline is going to get for those preflop decisions.
Go back to the awesome Texas Hold'em Strategy.
Comments

