Working Out Odds For Uncommon Draws

Okay, so you know how to work out the odds for hitting a flush draw or a straight draw. In fact, every pot odds article you've ever read uses either a flush or a straight draw (or both if you're lucky) as their main example to help explain how it all works.
- The odds of hitting a flush draw on the turn are 4.2 to 1.
- The odds of hitting a straight draw on the turn are 4.9 to 1.
Easy stuff. But what if you're draw isn't a straight or flush draw? What about if your draw is a combination of both? Or how about if you're drawing to something unusual/random like four of a kind?
In this article I'll show you the method for working out the odds for uncommon draws in Texas Hold'em. I'll also throw in a bunch of examples for good measure.
The method for working out odds of random draws.
The method for working out unusual draws is exactly the same as the method for working out standard flush or straight draws.
You find out how many outs you have, then compare that number of outs to the number of cards that won't help you (e.g. “non-outs” : ”outs”).
Note: “Outs” are cards that will complete the draw you are chasing after. (e.g. if you are after the last Ace to make 4-of-a-kind, you only have 1 out).
The important part here is just find the number of outs you have. After you've figured that out, the rest is a doddle. If you're not familiar with the basic process, I'd highly recommend you have a read through the main pot odds article first. But for the rest of you, I'm going to use the following steps:
- Find out how many unknown cards there are in total.
- Find out how many outs we have.
- Make ratio of outs to non-outs.
- Simplify that ratio to make it easier to work with.
Examples of working out odds for different types of drawing hands.
1) Flush draw on the turn.
We'll start with something simple.
Our hand: A![]() 2
2![]()
Board: K![]() 9
9![]() 7
7![]() 3
3![]()
In this example, we have a flush draw, but we're on the turn instead of the flop. Therefore, there will be one less unknown card than usual to include in our workings out.
- Total number of unknown cards = 46
- 2 cards in our hand.
- 4 cards on the board.
- 52 (total number of cards in a deck) minus 6 = 46.
- Total number of outs = 9
- There are 13 hearts in the deck.
- 2 of them are in our hand.
- 2 of them are on the board.
- Ratio = 37:9
- Out of 46 unknown cards, if we take away 9 outs we are left with 37 unwanted cards.
- Simplified ratio = 4.1:1
Easy! The only difference that you have to remember in this example is that we are on the turn and not the river. As a result, there is one less “unknown” card left in the deck due to the fact that we can now see the turn card.
The majority of examples work out odds for when you're on the flop waiting for the turn, so I thought I'd do one for when you're on the turn waiting for the river.
2) Flush draw + inside straight draw on the flop.
Our hand: A![]() 2
2![]()
Board: K![]() T
T![]() Q
Q![]()
In this example we have a standard nut flush draw, but we also have an inside straight draw to boot.
- Total number of unknown cards = 47
- 52 minus 5 cards we can see (2 in our hand and 3 on the flop).
- Total number of outs = 12
- 9 hearts left in the deck.
- 3 jacks. Don't forget that the J
 has been included in the 9 hearts above for the flush draw.
has been included in the 9 hearts above for the flush draw. - Ratio = 35:12
- 47 - 12 = 35.
- Simplified ratio = 2.9:1
The important part here is to remember that one of the jacks has already been included as an out for our flush draw. Many players make the mistake of believing that they have 9 hearts + 4 jacks, thinking they have 13 outs instead of 12.
Always double check to make sure that you're not including your outs twice when they can overlap like in this example.
3) Flush draw + 3-of-a-kind draw on the turn.
Our hand: A![]() 2
2![]()
Board: K![]() 9
9![]() 7
7![]() 2
2![]()
Let's say that we are confident that our opponent only has a pair or two-pair at best. Therefore, if we can improve our pair of twos to 3-of-a-kind, we will be able to win the hand (as well as if we are able to make a flush).
- Total number of unknown cards = 46
- Total number of outs = 11
- 9 hearts left in the deck.
- 2 twos.
- Ratio = 35:11
- 46 - 11 = 35.
- Simplified ratio = 3.2:1
This one's pretty straightforward. There are 2 twos left in the deck, and neither of them are hearts so we don't have to worry about these 2 outs overlapping with our flush draw outs.
4) Straight draw on the flop, and flush cards do not help us.
Our hand: Q![]() J
J![]()
Board: K![]() T
T![]() 2
2![]()
In this example we have a common open-ended straight draw. However, the problem is that there is also a flush draw on the flop. We are confident that our opponent has either top pair (or better) or a flush draw. This means that we are not interested in continuing with our hand if another spade comes on the turn. Therefore, the A![]() and 9
and 9![]() are not going to be considered as outs.
are not going to be considered as outs.
- Total number of unknown cards = 47
- Total number of outs = 6
- 8 straight draw outs in total (4 nines and 4 aces).
- Minus the A
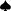 and 9
and 9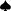 = 6.
= 6. - Ratio = 41:6
- 47 - 6 = 41.
- Simplified ratio = 6.8:1
Thanks to the flush draw cards our straight draw odds become a lot worse. We could just work out our normal straight draw odds including the spade cards (4.9:1) and then try to account for reverse implied odds as best as we can. However, this method is a lot simpler.
Final thoughts on working out odds for unusual draws.
Working out your odds of completing unusual draws and random types of hands all boils down to finding your total number of outs. After that, all you have to do is work through a small number of simple steps and you're done.
If you can figure out the exact number of outs you have, you'll never have a problem with odds.
Just remember:
- Find out how many outs you have.
- Make a ratio of non-outs to outs and simplify it.
Using this method you should be able to work out the odds in other random situations like:
- When the dealer accidentally flips over a card and has to burn it in a live game.
- When a player announces what cards they held before the hand is over.
- When you want to work out the odds of improving from 3-of-a-kind to 4-of-a-kind, because I mentioned it at the start of this article but didn't actually give an example (hint: you only have 1 out).
Note: After working your odds out you can compare your results with the list of odds found in the ratio odds chart.
Also, throughout this “unusual draws and their odds” article I've just worked out the ratio odds for different types of draws. If you're more comfortable using percentage odds, you can just use the same number of outs as before and use the rule of 2 and 4 to get a rough idea of your percentage odds.
Still struggling with playing flushes (and flush draws) in cash games? Try watching SplitSuit's strategy video on playing Flushes and Flush Draws.
Go back to the interesting Texas Hold'em Articles.
Can You Afford Not To Use
Poker Tracker 4?
“I wouldn’t play another session of online poker without it”
“I play $25NL, and in under 1 week PT4 had paid for itself”
Comments

