How To Use The Independent Chip Model (ICM).

Try out my free ICM calculator "CHIMP" to work out ICM in SNGs. It's a really handy ICM program.

How To Use ICM In Poker In my previous article that answered the question "what is ICM in Poker?" we found out that different chip stack sizes had varying amounts of equity in the overall tournament prize pool. To echo the last article's chip stacks example:

Player A - 5,000 chips.
Player B - 2,500 chips.
Player C - 2,500 chips.

Each player had the following amount of $ equity in the $100 prize pool that paid $50 for 1st, $30 for 2nd, and $20 for 3rd.

Player A: (5,000 chips) = $38.33 equity.
Player B: (2,500 chips) = $30.83 equity.
Player C: (2,500 chips) = $30.83 equity.

In this article I will show you how you can use these ICM equity numbers to work out whether or not to call all-ins from other players as we approach the money positions in Texas Holdem Sit and Go's.

cEV and $EV.

First things first, we need to understand the difference between cEV (chip EV) and $EV (money EV) in Sit and Go tournaments. As you should (hopefully) already know, EV standard for "Expected Value".

cEV is the amount of tournament chips we expect to gain/lose from a play.
$EV is the amount of tournament equity or money we expect to gain/lose from a play.

cEV.

Chip EV is like standard EV in cash games. For example, if your opponent pushes all in for 1,000 chips with AQ and you call with AK, you expect on average to make 480 chips every time you call this all in (I worked this out with some basic EV calculations).

Chip EV is just as you would expect - it's simply how many tournament chips you expect to gain on average from each play you make.

$EV

$EV is like a slightly advanced version of cEV, as $EV indicates how much extra money you expect to gain in prize pool equity from the tournament from each play you make.

For example, if you call an all-in with AK against AQ like in the cEV example you may earn +480 chips, but now that you've added those extra 480 chips to your stack how much more equity do you have in the overall prize pool? To put it another way, how much more likely are you to win money from the tournament with those extra 480 chips?

This is the difference between cEV and $EV, where $EV is going to be a far more profitable way to look at expected value in tournaments. $EV is pretty much the whole basis of the article, so do not worry if you do understand what I mean by this term just yet. It will become clearer as we go along.

Using ICM when faced with tough decisions.

When faced with a tough decision, we want to work out whether calling increases our overall prize pool equity.

For example, if we have ATo in the BB and the SB pushes all in with any random hand, we don't care about how many tournament chips we expect to win on average by calling, we just want to know whether calling increases our prize pool equity.

After all, we're not going to want to risk our chances of finishing in the money by placing ourselves in a situation that's only slightly better than a coin flip. So this is where we use ICM to work out whether making a big call near or on the bubble is profitable over the long run.

Using ICM example.

Lets say we are playing in a standard 10 player, $10+$1 tournament at PokerStars with a $100 prize pool that pays; $50 for 1st, $30 for 2nd, and $20 for 3rd. Following on from the previous example, there are 4 players left at the table and we are in the BB holding ATo.

The blinds are 100 / 200 and the stack sizes are as follows:

(HERO BB) Player A - 2,000
(SB) Player B - 2,000
(BTN) Player C - 2,500
(CO) Player D - 3,500

Everyone folds to the SB who pushes all in for 2,000 chips. We know for a fact that this guy is stupidly aggressive and could well be pushing all-in with any two cards. So should we call or should we fold? Well, we need to do 3 things:

Work out our equity against our opponent's range.
Work out the changes in prize pool equity for the different outcomes (of calling and winning/losing or folding).
Work out if we increase our prize pool equity by calling.

1) Work out our equity.

Let's start with the basics and work out the % chance of winning our ATo hand has against our opponent's any 2 cards. If we input this in to PokerStove we find that our hand has 62.7% equity against their range.

See the articles on range and range equity for more information on this particular topic.

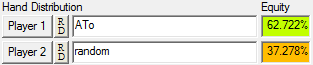
PokerStove ICM Results

Therefore, we can say that:

There is a 62.7% chance that we will increase our stack to 4,000 chips.
There is a 37.3% chance that we will lose all of our chips and leave the tournament with nothing.

Calling seems a little bit risky already, but let's move on to the next step to see whether or not it's actually going to be profitable to make this call over the long run.

2) Work out the different changes in prize pool equity.

To work this out we are going to require the use of our trusty ICM calculator. To work out the change in our prize pool equity and which action is most profitable, we will need to work out 3 things:

Our equity if we call and win.
Our equity if we call and lose.
Our equity if we fold to the all-in.

In the following quick examples I'm going to omit the blinds. I could include them, but it just makes following the example a lot easier for you if I leave them out for now.

Our equity if we call and win.

If we call and win, our chip stack increases to 4,000 and Player B gets knocked out. Using the ICM calculator the new prize pool equity between the 3 players would be:

Player A: (4,000 chips) = $35.49 equity. <- Our prize pool equity if we call and win.
Player B: (0 chips) = $0 equity.
Player C: (2,500 chips) = $30.51 equity.
Player D: (3,500 chips) = $34 equity.

Our equity if we call and lose.

If we lose we are out of the tournament, so as you can guess our prize pool equity will be $0. I'll post the equity results anyway just to keep things consistent.

Player A: (0 chips) = $0 equity. <- Our prize pool equity if we call and lose.
Player B: (4,000 chips) = $35.49 equity.
Player C: (2,500 chips) = $30.51 equity.
Player D: (3,500 chips) = $34 equity.

Our equity if we fold.

If we fold, our equity decreases a little because of the 200 chips we had to put in for the big blind.

Player A: (1,800 chips) = $20.29 equity. <- Our prize pool equity if we fold to the all-in.
Player B: (2,200 chips) = $23.48 equity.
Player C: (2,500 chips) = $25.50 equity.
Player D: (3,500 chips) = $30.73 equity.

3) Work out if we increase our prize pool equity by calling.

So then, which action is more profitable? Calling or folding?

If we fold, our equity drops to $20.29.

If we call, 63% of the time we are going to move our equity up to $35.49 and 37% of the time our equity will drop to $0. So if we calculate our average total prize pool equity from calling we get:

Total prize pool equity = (0.63 * 35.49) + (0.37 * 0) = $22.36.

So, comparing the two:

Folding = $20.29.
Calling = $22.36.

As you can see, our overall prize pool equity increases by calling this all-in bet. Therefore, it is more profitable to call with ATo over the long run against any random hand than it is to fold and save our chips. Even though on average every time we call we are only earning an extra $2.07, calling remains as the optimum play in this particular situation.

If your total prize pool equity decreases by calling, you should fold.

If your total prize pool equity increases by calling, you should call.

Evaluation of using ICM in Sit and Go tournaments.

Now I know what you're all thinking... how the hell am I supposed to work all of this out in the middle of a tournament? Well, in all honesty you can't, but this doesn't mean that learning about ICM has no value.

Making decisions using the independent chip model and prize pool equity is useful for post-game analysis and helping you to gauge risk vs. reward situations near the bubble. ICM is basically the theory behind the common concern of "is it worth risking all my chips in this spot?". The more you familiarize yourself with this concept, the more adept you will be at making the correct play in tricky situations.

I know that this has been a pretty long article, but trust me, if I could have made it any shorter I would have done! All ICM decisions boil down to at the end of the day are the 2 simple steps of working out your equity against your opponent's hand range, then working out whether your prize pool equity increases or decreases by calling.

To reiterate the two important concluding points of using ICM: