How To Calculate Expected Value - Boxes Method

Learning how to calculate expected value in poker can seem like a daunting task. It’s one of those topics that you put off learning, simply because it always seems a little too tricky to try and get your head around. But to be honest, when you see equations like this…

EV = ($1.60 x 0.4) + { 0.6 x [ ($2.80 x 0.05) + (-$1.20 x 0.9) ] }…I don’t blame you for walking away. That kind of stuff makes Bill Chen’s The Mathematics of Poker look like The Very Hungry Caterpillar.
So, here’s my attempt at helping you get your expected value calculations nailed down once and for all. I’m going to try and make it easier for you to visualize the process with my "boxes method". No more running away from math strategy articles and forum threads.
The three steps to calculating expected value.
In poker, you calculate expected value for a specific action. For example; what is the EV of calling? What is the EV of folding? What is the EV of raising? — Those are specific actions.
Once you’ve decided what action you want to calculate the EV of, you just need to follow these 3 simple steps:
- The 3 steps to calculating EV (with the boxes method).
- List all the possible outcomes of that action. (Make the boxes)
- Find the probability and the win/loss of each outcome. (Fill the boxes)
- Put it all together in an equation and work it out. (Solve the boxes)
Let’s run through an actual example, and I’ll explain each step as we go along.
The example hand situation.
We are playing $100NL against a useless short stack player. We raise to $4 with A![]() K
K![]() from MP and this short stack player in the SB is the only caller.
from MP and this short stack player in the SB is the only caller.
Flop: K![]() 7
7![]() 4
4![]()
Pot: $9
The short stack immediately moves all-in for $6 (yep, $6). After doing so, they also turn over their hand to show us 6![]() 5
5![]() — they have a flush draw and a straight draw. So the situation is as follows:
— they have a flush draw and a straight draw. So the situation is as follows:
Hero: A![]() K
K![]()
Villain: 6![]() 5
5![]()
Flop: K![]() 7
7![]() 4
4![]()
Pot: $15
We have to call $6 to continue. What is the EV of calling?
Step 1 - List all the possible outcomes. (Make the boxes)
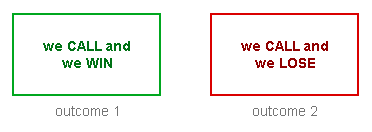
If we call this $6 bet, what can happen? Well, two things:
- We call and end up winning.
- We call and end up losing.
These are the only two possible things that can happen after we call. Easy stuff.
However, there are not always just two outcomes. There could be more or there could be less depending on the situation. Either way, it’s a nice idea to think of each outcome as it’s own separate “thing” -- or as I like to do, give it an imaginary box:
Step 2 - Find the probability and win/loss of each outcome. (Fill the boxes)
Okay, so we’ve got our two outcomes. Now we just need to find the probability of each outcome happening, and the amount of money we win or lose when it does happen. Let’s work these out for each of the two outcomes one at a time.
1) We call and we end up winning.
The probability.
How do we work out the probability of winning in this situation? The easiest way is to just plug the cards in to PokerStove.
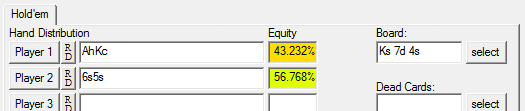
This shows us that our probability of winning when we call is 43%.
The win/loss.
If we call and win, we win the $15 in the pot.
The $15 currently in the pot is our prize. We do not count our $6 call in this amount because it belongs to us, and we cannot win what we already own.
Note: It’s important to make the distinction between money that is yours to lose and money that is in the pot. They are two separate things. Don’t get hung up on any amount of money you may have put in to the pot earlier on in the hand -- it doesn’t matter.
2) We call and we end up losing.
The probability.
If we look at the same PokerStove results as before:

We can see that the probability of losing when we call is 57%.
The win/loss.
If we call and lose, we will lose our $6 call.
The only amount of money we are losing is our $6 call. Sure, we’ve already put money in to the pot, but don’t think of that as “belonging” to us anymore. It now belongs to the pot, so it’s not something we can lose.
Tidying up step 2.
-
Outcome 1 - we call and we win.
- Probability = 43%
- Win/loss = +$15
-
Outcome 2 - we call and we lose.
- Probability = 57%
- Win/loss = -$6
Remember how we’ve already put these outcomes as separate boxes? Well, let’s fill these boxes with this new information.

Step 3 - Put it all together in an equation and work it out. (Solve the boxes)
To form our EV equation, all we need to do is multiply the probability by the win/loss in each of the boxes, then add all the boxes together.
So, still using these boxes, our equation looks like this:
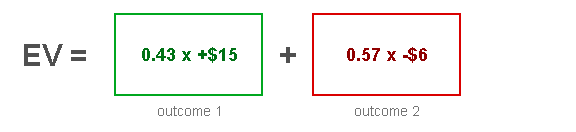
Now just work out the answers for each box:
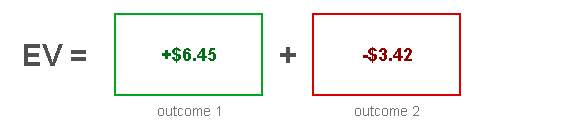
Finally, add them all together and we get the answer to our EV calculation:
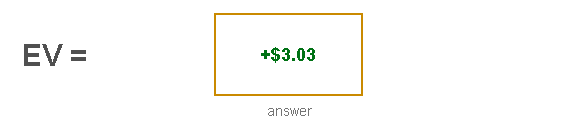
So the EV of calling with AK is +$3.03. Every time we make this call, we win $3.03 on average. Therefore, calling -- as opposed to folding (we make $0 by folding)-- is the correct play.
This amount of money could also be referred to as $3.03 Sklansky Bucks.
It doesn’t feel very mathematical using all those boxes though. How can we show it in a more "mathematical-looking" way?
Answer: Just replace the boxes with brackets, like this:
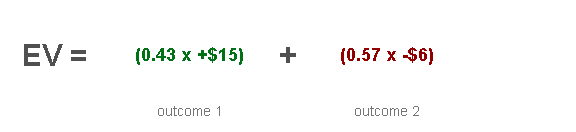
EV = ($6.45) + (-$3.42)
EV = +$3.03
Note: Notice how we only had 43% chance to win the hand (or 43% "equity"), yet calling is still +EV? That’s all thanks to the good pot odds we are getting when our opponent bets all-in for $6 in to a $9 pot on the flop.
Final thoughts.
I hope that nobody feels patronized by my “box method” for working out EV in poker. It’s just that ever since I started thinking about expected value calculations in terms of “chunks” or “boxes”, it all became much easier. It may not be for everyone, but if this box method for calculating expected value works for you, then I’m glad to have shared it.
This method is also easily extensible. If there is a situation where there are more than 2 outcomes, just add more boxes. The boxes are just there to split everything up and make EV calculations easier to digest.
In all honesty, the only difficult thing about calculating expected value is the notation. The actual method is surprisingly straightforward, and my primary hope is that this article has helped to highlight that fact.
Go back to the awesome Texas Hold'em Strategy.
Comments

